Contoh Soal Deret Geometri Dan Penyelesaiannya
Contoh Soal Deret Geometri dan Penyelesaiannya | Kesempatan kali ini saaya akan menunjukkan soal deret geometri dan pembahasannya. Materi inii merupakan salah satu bahan yang sangat penting pada mata pelajaran matematika. Oleh alasannya ialah itu temen-temen sebaiknya tidak meninggalkan membahas soal-soal. Berikut ini ialah sedikit klarifikasi wacana Deret Geometri.
Apa itu Deret Geometri ?
Sama halnya menyerupai deret aritmatika yang merupakan jumlah dari barisan aritmatika, maka deret geometri ialah hasil penjumlahan dari nilai suku suku sebuah barisan geometri. Deret geometri dikenal juga dengan sebutan deret ukur. Oke, eksklusif saja simak beberapa referensi soal berikut ini.
Contoh Soal Deret Geometri dan Penyelesaiannya I
sumber : matematika-go.blogspot.com
Jumlah dari n suku pertama suatu barisan geometri disebut sebagai deret geometri. Jika suku ke-n dari barisan geometri dirumuskan: an = a1rn – 1, maka deret geometri sanggup dituliskan sebagai,Jika kita mengalikan deret tersebut dengan –r kemudian menjumlahkannya dengan deret aslinya, kita mendapatkan
Sehingga kita memperoleh Sn – rSn = a1 – a1rn. Dengan menuntaskan persamaan tersebut untuk Sn, kita mendapatkan
Rumus suku ke n

Contoh Soal:
- Tentukan jumlah 10 suku pertama dari deret 32 + 16 + 8 + ….!
- Tentukan nilai n yang memenuhi2 + 22 + 23 + ….. + 2n = 510!
1. Dari deret 32 + 16 + 8 + .... didapat a = 32 dan r = 1/2, sehingga
2. Dari deret 2 + 22 + 23 + ….. + 2n = 510 didapat a = 2 dan r = 2, sehingga
Soal No. 3
Diberikan sebuah deret geometri sebagai berikut.
3 + 6 + 12 + ....
Tentukan suku ke-5 dari deret tersebut!
Pembahasan
Rumus suku ke-n deret geometri
Un = arn −1
a = suku pertama
r = rasio
Dari soal
a = 3
r = 6/3 = 2
sehingga
Un = arn−1
U5 = 3 (2)5 −1 = 3 (2)4 = 3(16) = 48
Soal No. 4
Diketahui suku pertama suatu deret geometri ialah 4 dengan suku ke-5 ialah 324. Tentukan rasio dari deret tersebut!
Pembahasan
Data dari soal di atas
U5 = 324
a = 4
Dari Un = arn −1

Dengan demikian rasionya ialah 3 atau − 3
Soal No. 5
Deret geometri 12 + 6 + 3 + ....
Tentukan U3 + U5
Pembahasan
U3 = 3
a = 12
r = 6/12 = 1/2
Un = arn −1
U5 = 12(1/2)5 −1 = 12(1/2)4 = 12(1/16) = 12/16 = 3/4
Sehingga
U3 + U5 = 3 + 3/4 = 3 3/4
Soal No. 6
Diberikan sebuah deret geometri sebagai berikut.
3 + 6 + 12 + ....
Tentukan jumlah 7 suku pertama dari deret tersebut!
Pembahasan
Data:
a = 3
r = 6/3 = 2
S7 =....
Rumus mencari jumlah n suku pertama deret geometri untuk rasio lebih besar dari satu r > 1
Sehingga:


Soal No. 7
Diberikan sebuah deret geometri sebagai berikut.
24 + 12 + 6 +...
Tentukan jumlah 7 suku pertama dari deret tersebut!
Pembahasan
Data:
a = 24
r = 12/24 = 1/2
S7 =....
Rumus mencari jumlah n suku pertama deret geometri untuk rasio lebih kecil dari satu r < 1
Sehingga:


soal no 8
Seutas tali dibagi menjadi 5 bab yang panjangnya membentuk barisan geometri.
Jika tali yang paling pendek ialah 10 cm dan tali yang paling panjang ialah 160 cm, tentukan panjang tali semula.
Jika tali yang paling pendek ialah 10 cm dan tali yang paling panjang ialah 160 cm, tentukan panjang tali semula.
Penyelesaian:
Diketahui potongan-potongan tali membentuk barisan geometri, dengan:
panjang tali terpendek = U1 = a = 10
panjang tali terpanjang = U5 = ar4 = 160
banyak bab tali = n = 5
panjang tali terpendek = U1 = a = 10
panjang tali terpanjang = U5 = ar4 = 160
banyak bab tali = n = 5
Ini berarti panjang tali semula ialah jumlah panjang kelima bab tali (S5).
Mula-mula tentukan nilai r dengan mengganti a = 10, n = 5 dan U5 = 160 ke rumus Un.

Selanjutnya tentukan panjang panjang tali semula (S5) yaitu
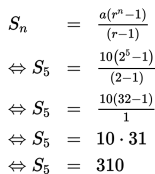
Jadi, panjang tali semula ialah 310 cm.
soal no 9
soal no 9
Sebuah bola dijatuhkan dari ketinggian 4 meter. Kemudian bola tersebut memantul kembali setinggi 3 meter dan seterusnya. Setiap kali menyentuh lantai, bola tersebut akan memantul setinggi 34 kali ketinggian sebelumnya. Tentukan panjang lintasan yang terbentuk hingga bola menyentuh lantai untuk yang ke-3 kalinya.
Penyelesaian:
Perhatikan gambaran berikut.

Berdasarkan ilustrasi, tampak bahwa ketika bola dijatuhkan dan menyentuh lantai untuk yang ke 3 kali sebetulnya bola tersebut mengalami 3 kali gerakan turun (panah merah) dan 2 kali gerakan naik (panah biru).
• Barisan yang terbentuk dikala bola turun (ditunjukkan oleh panah warna merah) ialah 4,(34 ) 4, (34)2 (4),... = 4, 3, 94 , ....
Barisan ini ialah barisan geometri turun dengan a = 4 dan r =34
Oleh alasannya ialah terdapat 3 kali gerakan turun (n = 3), maka panjang lintasan yang terbentuk dikala bola turun (S3) adalah
Oleh alasannya ialah terdapat 3 kali gerakan turun (n = 3), maka panjang lintasan yang terbentuk dikala bola turun (S3) adalah
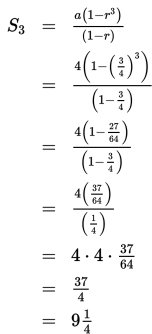
- Barisan yang terbentuk dikala bola naik (ditunjukkan oleh panah warna biru) ialah (
34 ) 4 ,(34)2 (4), ... = 3,94 , ....
Barisan ini ialah barisan geometri turun dengan a = 3 dan r =
Oleh alasannya ialah terdapat 2 kali gerakan naik (n = 2), maka panjang lintasan yang terbentuk dikala bola naik (S2) adalah

Jadi, panjang lintasan yang terbentuk hingga bola menyentuh lantai untuk yang ke 3 kalinya ialah 14, 5 meter.
Soal Deret Geometri dan Pembahasannya II
sumber : rumus-matematika.com
Soal 1.
Tunjukkan bahwa 2+(-6)+18+(-54)+162+ … merupakan deret geometri atau deret ukur !
Penyelesaian :
Syarat deret geometri yaitu mempunyai rasio yang tetap.
r = U2/U1 = -6/3 = -3
r = U3/U2 = 18/-6 = -3
r = U4/U3 = -54/18 = -3
r = U5/U4 = 162/-54 = -3
Karena rasionya selalu tetap yaitu -3, maka 2+(-6)+18+(-54)+162+ … merupakan deret geometri atau deret ukur.
Soal 2
Tentukan suku ke-7 dari deret 5+10+20+40+… !
Penyelesaian :
U1 = 5
n = 7
r = 2
Suku ke-n = U1 × rn-1
Suku ke-7 = 5 × 27-1
= 5 × 26
= 5 × 64
= 320
Soal 3.
Tentukan banyak suku dari deret -3+6+(-12)…+96!
Penyelesaian :
U1 = -3
Un = 96
r = 6/-3 = -2
Un = U1 × rn-1
96 = -3 × (-2)n-1
(-2)n-1 = 96 : (-3)
(-2)n-1 = -32
(-2)n-1 = (-2)5
n-1 = 5
n = 6
Jadi, banyak suku pada deret tersebut = 6.
Soal 4.
Dalam suatu deret geometri diketahui U1 = 6 dan U5 = 486. Tentukan besar rasionya ?
Penyelesaian :
U1 = 6
U5 = 486
n = 5
Un = U1 × rn-1
U5 = 6 × r5-1
486 = 6 × r4
r4 = 486/6
= 81
r = 3 atau -3
Sehingga rasio deret tersebut yaitu 3 atau -3.
Soal 5.
Dalam suatu deret geometri diketahui U3 = 81 dan U6 = 3. Tentukanlah deret tersebut !
Penyelesaian :
U3 = 81, maka U1 × r² = 81
U6 = 3, maka U1 × r5 = 3
U6/U3 = ( U1 × r5 )/( U1 × r² ) = 3/81
r³ = 1/27
r = akar pangkat 3 dari (1/27)
r = 1/3
U1 × r² = 81
U1 × (1/3)² = 81
U1 × 1/9 = 81
U1 = 81 : 1/9
U1 = 81 × 9
U1 = 729
Kaprikornus deret tersebut ialah 729+243+81+27+…
Soal 6.
Suku pertama suatu deret geometri ialah 2 dan rasionya ialah 3. Jika suku tengah deret tersebut = 54, tentukanlah :
a. suku terakhir dari deret tersebut.
b. banyak suku pada deret tersebut.
Penyelesaian :
a. U1 = 2
Ut = 54
r = 3
Ut = √(U1×Un)
54 = √(2×Un)
54² = 2×Un
2.916 = 2Un
Un = 2.916/2
Un = 1.458
Jadi, suku terakhir (Un) dari deret tersebut yaitu 1.458.
b. Un = U1 × rn-1
1.458 = 2 × (3)n-1
(3)n-1 = 1.458/2
(3)n-1 = 729
(3)n-1 = 36
n-1 = 6
n = 7
Maka banyak suku pada deret tersebut ialah 7.
Demikianlah Contoh Soal Deret Geometri dan Penyelesaiannya. Semoga bermanfaat. Selamat berguru dan lupa share artikel ini kepada sahabat - temanmu.
Demikianlah Contoh Soal Deret Geometri dan Penyelesaiannya. Semoga bermanfaat. Selamat berguru dan lupa share artikel ini kepada sahabat - temanmu.
Sumber http://www.contohsoaljawab.com/







0 Response to "Contoh Soal Deret Geometri Dan Penyelesaiannya"
Posting Komentar